CHAPTER 7
1. Pendahuluan[kembali]
Rangkaian aritmatik adalah bagian penting dalam sistem digital yang digunakan untuk melakukan operasi matematis seperti penjumlahan, pengurangan, dan manipulasi data biner. Rangkaian ini disusun dari kombinasi gerbang logika dasar dan digunakan dalam berbagai perangkat digital, termasuk kalkulator, prosesor, dan mikrokontroler. Mempelajari rangkaian aritmatik membantu memahami cara kerja pengolahan data dalam bentuk biner serta menjadi dasar dalam perancangan sistem digital yang lebih kompleks.
2. Tujuan [kembali]
- Mempelajari dan memahami konfigurasi rangkaian aritmatika.
- Memahami cara pembuatan rangkaian aritmatika pada proteus.
- Mengetahui penggunaan rangkaian aritmatika.
3. Alat dan Bahan [kembali]
- IC 7485
IC 7485 4-bit Magnitude Comparator adalah komparator 4-bit yang digunakan untuk membandingkan dua bilangan biner 4-bit, yaitu A (A3–A0) dan B (B3–B0).
IC ini menghasilkan tiga sinyal output: A > B A = B A < B
jenis pertama adalah gerbang AND. Gerbang AND ini memerlukan dua atau lebih input untuk menghasilkan satu output. Jika semua atau salah satu inputnya merupakan bilangan biner 0, maka outputnya akan menjadi 0. Sedangkan jika semua input adalah bilangan biner 1, maka outputnya akan menjadi 1.
Jenis kedua adalah gerbang OR. Sama seperti gerbang sebelumnya, gerbang ini juga memerlukan dua input untuk menghasilkan satu output. Gerbang OR ini akan menghasilkan output 1 jika semua atau salah satu input merupakan bilangan biner 1. Sedangkan output akan menghasilkan 0 jika semua inputnya adalah bilangan biner 0.
Jenis berikutnya adalah gerbang XOR. Gerbang XOR ini memerlukan dua input untuk menghasilkan satu output. Jika input berbeda (misalkan: input A=1, input B=0) maka output yang dihasilkan adalah bilangan biner 1. Sedangkan jika input adalah sama maka akan menghasilkan output dengan bilangan biner 0.
Jenis berikutnya adalah gerbang NOT. Gerbang NOT ini berfungsi sebagai pembalik keadaan. Jika input bernilai 1 maka outputnya akan bernilai 0 dan begitu juga sebaliknya.
4. Dasar Teori [kembali]
-
Difference (D) , hasil pengurangan A - B
A ⊕ B (XOR)-
Borrow (Bo) , bit pinjaman jika A < B
 | |||
|---|---|---|---|
Persamaan Logika
Penjelasan
|
5. Example [kembali]
A= 1, B= 0
Difference (D) = A ⊕ B = 1 ⊕ 0 = 1
-
Borrow (Bo) = ¬A ∧ B = ¬1 ∧ 0 = 0 ∧ 0 = 0
Jawaban:
-
Difference = 1
-
Borrow = 0
(Artinya: 1 - 0 = 1, tidak butuh pinjaman)
2. Example
A = 0, B = 1
-
Difference (D) = A ⊕ B = 0 ⊕ 1 = 1
-
Borrow (Bo) = ¬A ∧ B = ¬0 ∧ 1 = 1 ∧ 1 = 1
Jawaban:
-
Difference = 1
-
Borrow = 1
(Artinya: 0 - 1 = -1 dalam bentuk biner, jadi hasilnya 1 dengan pinjaman 1)
6. Problem [kembali]
1. Problem
Implementasikan perangkat keras pembanding magnitudo 3-bit yang memiliki satu keluaran yang bernilai TINGGI ketika dua bilangan 3-bit sama. Gunakan hanya gerbang NAN
Solusi:
Kondisi ekivalensi dari dua bilangan tiga bit diberikan oleh persamaan X = x2, x1, x0, di mana x2 = A2B2 + A2B2, x1 = A1B1 + A1B1, dan x0 = A0B0 + A0B0.
Gambar di bawah menunjukkan diagram logika. x2, x1, dan x0 masing-masing diberikan oleh operasi EX-NOR dari (A2, B2, (A1, B1, dan (A0, B0). Persamaan-persamaan ini kemudian di-AND untuk mendapatkan X
2. Problem
Rancang magnitudo comparator dua-bit. Tulis juga ekspresi Boolean yang relevan.
Solusi:
Misalkan A(A1A0) dan B(B1B0) adalah dua bilangan. Jika X, Y, dan Z masing-masing mewakili kondisi A=BA>B dan A<B (yaitu, X=1, Y=0, dan Z=0 untuk A=B; X=0, Y=1, dan Z=0 untuk A>B; dan X=0, Y=0, dan Z=1 untuk A<B), maka ekspresi untuk X, Y, dan Z dapat ditulis sebagai berikut:
Gambar dibawah menunjukkan diagram logika 2-bit comparator
7. Soal Pilihan Ganda [kembali]
1. Diberikan dua input A = 1 dan B = 1. Berapakah Difference (D) dan Borrow (Bo) pada rangkaian Half-Subtractor?
2. Manakah persamaan yang benar untuk menghitung Borrow (Bo) dalam rangkaian Half- Subtractor?
A. Bo = A ∧ B
B. Bo = A ⊕ B
C. Bo = ¬A ∧ B
D. Bo = A ∨ B
8. Percobaan [kembali]
a) Prosedur[kembali]
- Buka aplikasi proteus
- Pilih komponen yang dibutuhkan, pada rangkaian ini dibutukan gerbang XOR, Gerbang AND, dan gerbabng OR.
- Rangkai setiap komponen menjadi rangkaian yang diinginkan
- Ubah spesifikasi komponen sesuai kebutuhan
- Jalankan simulasi rangkaian
b) Rangkaian Simulasi dan Prinsip Kerja [kembali]
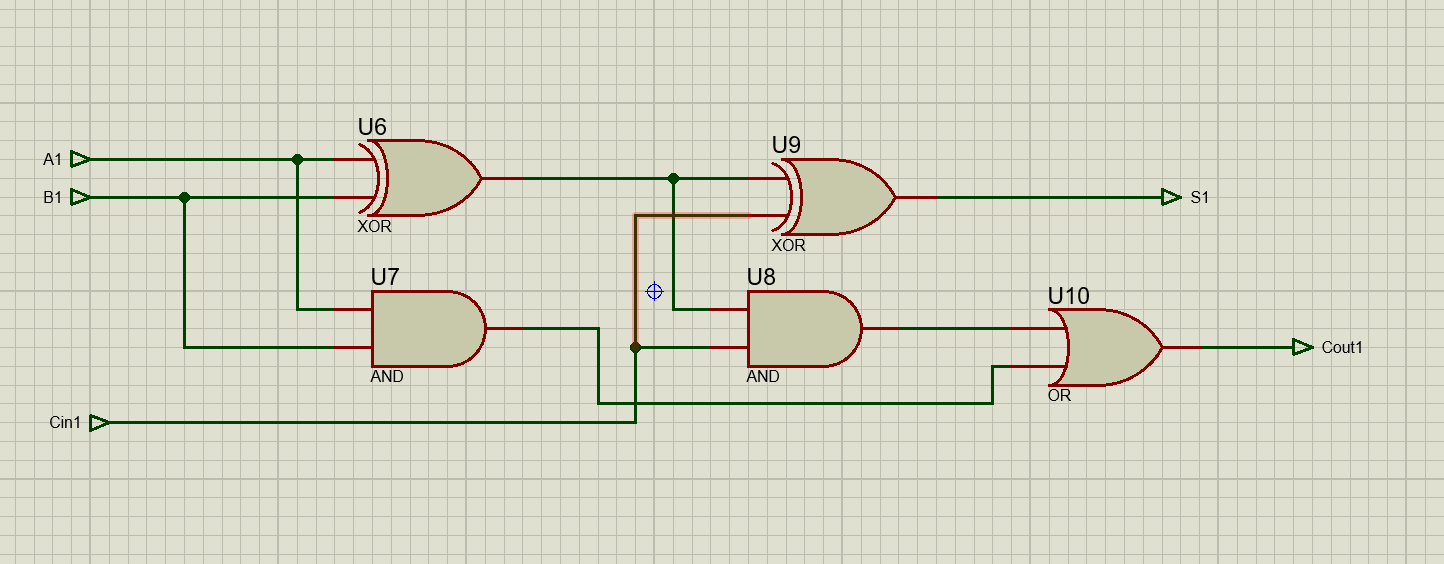

A1, B1, dan Cin1 (carry input), serta dua output yaitu S1 (sum) dan Cout1 (carry output). Proses penjumlahan dimulai dari gerbang XOR pertama (U6) yang menghitung A1 ⊕ B1, menghasilkan sum sementara. Output dari XOR ini kemudian diproses bersama Cin1 melalui XOR kedua (U9) untuk menghasilkan output sum final S1. Sementara itu, gerbang AND pertama (U7) menghitung A1 ∧ B1, dan gerbang AND kedua (U8) menghitung (A1 ⊕ B1) ∧ Cin1. Hasil dari dua gerbang AND ini dikombinasikan oleh gerbang OR (U10) untuk menghasilkan Cout1, yaitu carry keluar. Dengan demikian, rangkaian ini secara keseluruhan berfungsi menjumlahkan tiga bit biner dan menghasilkan satu bit hasil serta satu bit carry.Ai dan Bi) serta carry input dari full adder sebelumnya. Rangkaian dimulai dari Full Adder 0 yang menerima input A0, B0, dan Cin0. Hasil sum (S0) dan carry output (Cout0) dari adder pertama diteruskan ke adder berikutnya, dan proses ini berlangsung hingga full adder terakhir (Full Adder 3) yang menghasilkan output sum terakhir (S3) dan carry akhir (Cout). Penjumlahan dilakukan secara bit-per-bit dari bit terkecil hingga terbesar dengan mempertimbangkan carry di setiap langkah. Nilai input biner yang digunakan dalam gambar menghasilkan output 0011 (desimal 3) dengan carry out akhir 1. Rangkaian ini menunjukkan bagaimana penjumlahan bilangan biner lebih dari 1-bit dapat dilakukan dengan prinsip full adder berantai.A sebagai minuend dan B sebagai subtrahend. Rangkaian ini memiliki dua output: Difference (D) sebagai hasil pengurangan dan Borrow (Bo) sebagai penanda apakah terjadi peminjaman saat pengurangan berlangsung. Pada kondisi input yang diberikan, yaitu A = 1 dan B = 0, maka operasi pengurangan yang terjadi adalah 1 dikurangi 0. Dalam logika biner, hasil dari 1 - 0 adalah 1 dan tidak memerlukan peminjaman, sehingga output yang dihasilkan oleh rangkaian ini adalah D = 1 dan Bo = 0. Secara logika, Difference diperoleh dari operasi XOR (A ⊕ B), sedangkan Borrow dihasilkan dari operasi ¬A ∧ B. Karena A bernilai 1, maka ¬A = 0, dan 0 ∧ 0 = 0, yang menghasilkan nilai Borrow = 0. Oleh karena itu, prinsip kerja Half-Subtractor ini dapat dijelaskan sebagai pengurangan satu bit yang menghasilkan nilai selisih dan informasi peminjaman berdasarkan nilai logika dari kedua input.A sebagai minuend (bilangan yang dikurangi) dan B sebagai subtrahend (pengurang). Tujuan dari rangkaian ini adalah menghitung hasil pengurangan satu bit biner (A - B) dan menentukan apakah terjadi pinjaman atau tidak. Output pertama, yaitu D (Difference), dihasilkan dari gerbang XOR (U1) yang mengimplementasikan operasi A ⊕ B. Output ini menunjukkan selisih biner antara A dan B. Output kedua, yaitu B0 (Borrow), dihasilkan dari gerbang AND (U2) yang menerima input dari hasil negasi A (melalui gerbang NOT U3) dan langsung dari B. Operasi ini merepresentasikan logika ¬A ∧ B, yang berarti borrow hanya terjadi jika A bernilai 0 dan B bernilai 1. Dengan kata lain, peminjaman diperlukan hanya ketika nilai yang dikurangkan (B) lebih besar dari nilai asal (A). Secara keseluruhan, rangkaian ini secara sederhana menjelaskan konsep pengurangan biner satu bit dengan menampilkan hasil pengurangan dan status pinjaman.c) Video Simulasi [kembali]
d) Download File [kembali]
- Download rangkaian 7.11 klik disini
- Download rangkaian 7.12 klik disini










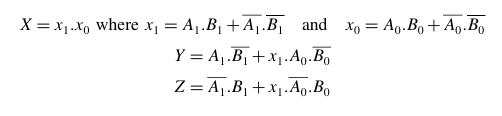




Komentar
Posting Komentar